Okay, hold up, what is a BST?
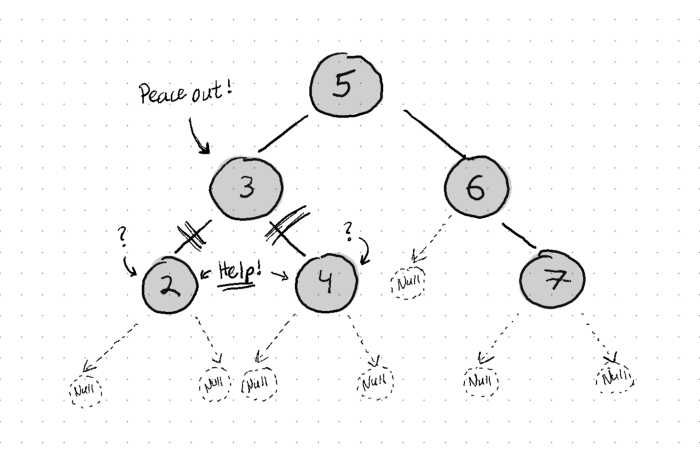
A Binary Search Tree is one of many tree structures in data science and also a popular implementation of the Dictionary ADT (associates keys with values). It is a binary tree, meaning that it is a rooted acyclic graph in which each node can have a maximum of two children (hence, binary). Children with keys ‘less than’ the parent are located in the left sub-tree, and children with keys ‘greater than’ the parent are stored in the right sub-tree. These comparisons are dictated by inequality operators (<,>,≥,≤), and the implementation may vary from language to language (how are strings/numbers/objects compared in C vs Python, Javascript?), but the general idea here holds. Below is an illustration of a basic BST with just the keys shown to demonstrate the organization of nodes.
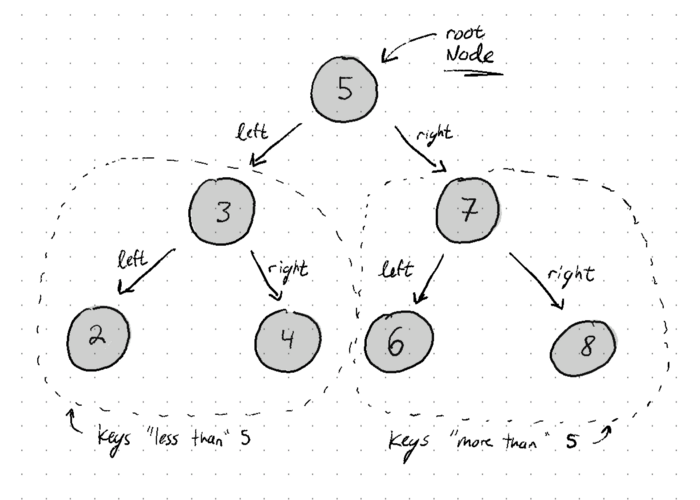
What’s special about a BST is that it is usually quite performant by definition. If you want to find where the key 4 is in the example above, you will start at the root. Because we know that keys ‘less than’ the current node are stored in the left sub-tree, we don’t even have to consider checking the right sub-tree (containing 7, 6, and 8); and thus, we can jump straight to node 3, then eventually 4 (disregarding the left sub-tree of 3 since 4 is greater). You can choose to read more about how balancing affects performance, but we wont bother ourselves with balancing in this article. Compare this to searching an array: Is the first entry what we are looking for? The second? Third?…. It’s important to understand that arrays can be indexed into at in O(1) time, but BSTs cannot since they are not stored contiguously in memory. BSTs really shine when you need to do range-based searches for data within the structure.
Getting Started
I’ll be using NodeJS 8.12 for this project. It supports ES6 class syntax, which is really nice for me. You can do the same with generator functions in ES5, but only if you’re comfortable with them. I’m not yet, and there’s no shame in admitting that, so Node 8.12 it is. You can also configure Babel for transpilation, but that’s a bit overkill and also beyond the scope of this article. I’ll start off by creating a new directory for the project files, and initializing (by preference) a package.json file (so that I can publish my work on NPM as a package for others to use easily) as well as Git version control (having source history is nice to track changes and revert boo-boos if need be).
$ mkdir BSTjs
$ npm init
$ git initNext, I made two files: BST.js and index.js. The former will hold our structure definition, and the latter will simply be used as our project entry-point and will provide a place to put some rudimentary tests.
BST.js will simply contain a bare class export, which we will implement later on. I have declared class methods for most of the ADT functions specified here. index.js imports the BST class and instantiates a new tree which is then logged to the console.
/**
* Used internally in the main BST class to store
* data in the tree structure. Each node represents
* a key/value pair in our BST.
*/
class BSTNode {
/* Initializes node storage upon creation: */
constructor(key, value) {
/* Internal variables for storing data: */
this.key = key;
this.value = value;
/* Used for storing references to left/right
children */
this.left = null;
this.right = null;
};
}
/**
* Main wrapper class for the BST data structure.
* Implements necessary ADT member functions for
* accessing, adding and removing data from the tree.
*/
class BST {
/* Creates a new BST object. */
constructor() {
/* Stores the root node of the tree */
this.root = new BSTNode(null, null);
/* Required for member functions to access
class member variables through current class
context using 'this' */
this.insert.bind(this);
this.find.bind(this);
this.remove.bind(this);
this.isEmpty.bind(this);
};
/* Inserts a new key/value pair into the BST. */
insert(key, value) { };
/* Finds the data associated with the supplied
key. Returns NULL if no such key is present. */
find(key) { };
/* Removes data with supplied key from the BST. */
remove(key) { };
/* Returns true if no data is in the BST, and false
if the structure stores data. */
isEmpty() { };
};
/* Export the BST class for use in other files */
module.exports = BST;const BST = require('./BST');
/* Create a new tree */
const tree = new BST();
/* Insert some key/values into the tree */
tree.insert('NodeJS', 'Node.js is an open-source, cross-platform JavaScript run-time environment that executes JavaScript code outside of a browser.');
tree.insert('Python', 'Python is an interpreted, high-level, general-purpose programming language.');
tree.insert('C++', 'C++ is a general-purpose programming language.');
tree.insert('Ruby', 'Ruby is a dynamic, interpreted, reflective, object-oriented, general-purpose programming language.');
tree.insert('Haskell', 'Haskell is a standardized, general-purpose, purely functional programming language with non-strict semantics and strong static typing.');
/* Remove C++ */
tree.remove('C++');
/* Get the definition of NodeJS */
console.log(`\nNodeJS Definition: ${tree.find('NodeJS')}\n`);
/* Pretty-print the tree to the console: */
console.log(`\nTree: ${JSON.stringify(tree, null, 2)}\n`);We can now run our code using node ./index.js, or if you setup your package.json file, npm start. It will spit out the following since we haven’t implemented any of the member functions yet:
NodeJS Definition: undefinedTree: {
"root": {
"key": null,
"value": null,
"left": null,
"right": null
}
}Implementing isEmpty:
Let’s start with the easiest method first. To implement isEmpty() all we need to do is check the root to see if its key is null. Since keys are essentially unique identifiers for the data stored in our tree, having a null key doesn’t mean much to the typical user, and thus, will be a good way for us to denote that the current BSTNode we’re evaluating is empty.
/* Returns true if no data is in the BST, and false
if the structure stores data. */
isEmpty() {
return this.root.key === null;
};Implementing insert:
Here is the current implementation of insertion into the Binary Search Tree:
/* Inserts a new key/value pair into the BST. */
insert(key, value) {
/* Lambda function to recursively find insertion node
and add data to that insertion point accordingly. */
const insertRecursive = (subRoot, key, value) => {
if (subRoot.key === null) {
/* We've reached the insertion point,
add the data here. */
subRoot.key = key;
subRoot.value = value;
/* Add sentinel nodes to the left/right fields */
subRoot.left = new BSTNode(null, null);
subRoot.right = new BSTNode(null, null);
} else {
if (key === subRoot.key) {
/* Key already exists in the tree. As per
implementation, replace existing node with
new insertion data */
subRoot.value = value;
} else {
/* We haven't reached the insertion point
yet and need to recurse deeper into the
tree. */
(key < subRoot.key)
? insertRecursive(subRoot.left, key, value)
: insertRecursive(subRoot.right, key, value);
}
}
};
/* Call insertion recursively on the root */
insertRecursive(this.root, key, value);
};There are a few things to note about this implementation:
- A recursive helper lambda function is defined on line 5, and we call it on the root BSTNode on line 32 with the key and value to insert into the tree.
- All objects other than base primitives (Strings, Numbers, Booleans, etc.) are passed by reference in Javascript. Here is a really good article by Naveen Karippai on this topic: Learning how references work in Javascript. This means that we can perform recursion on instances of BSTNode classes (such as root, left/right children) since classes are basically just glorified generator functions, and are therefore passed by reference. This recursion can be seen when we pass subRoot as a parameter to our insertRecursive lambda function on line 5. When we update the values of subRoot’s key and value fields on lines 9 and 10, this will directly modify the data that lives in our tree since subRoot is a reference to the BSTNode located inside the tree and not a local copy made on Javascript’s function stack.
- On lines 12 and 13, we ensure that our newly added node has defined left and right BSTNodes instead of assigning them to null. This was done because nulls are considered primitives in Javascript, and if we perform recursion on them in lines 25 and 26, then any updates we do will be on local copies on the function stack and thus wont be reflected in our tree structure. By assigning them ‘dummy’ nodes with a key/value of null, we have a way to denote that a leaf isn’t technically present at that spot, but they can still be passed by reference.
- For this implementation, if we try to insert new data at a key that already exists, then we will replace any existing data for that key. This is a design decision that I feel makes sense for 90% of use cases. This can be seen in lines 15–19.
- Recursion is performed on lines 24–26 based upon the fact that keys less than the current node’s key are stored in the left sub-tree, and in the right sub-tree otherwise. A ternary expression is used for simplification.
Now that we can insert into the tree, our output should show the correct BST hierarchy (but with C++ still present because we haven’t implemented remove yet…)
NodeJS Definition: undefined
Tree: {
"root": {
"key": "NodeJS",
"value": "Node.js is an open-source, cross-platform JavaScript run-time environment that executes JavaScript code outside of a browser.",
"left": {
"key": "C++",
"value": "C++ is a general-purpose programming language.",
"left": {
"key": null,
"value": null,
"left": null,
"right": null
},
"right": {
"key": "Haskell",
"value": "Haskell is a standardized, general-purpose, purely functional programming language with non-strict semantics and strong static typing.",
"left": {
"key": null,
"value": null,
"left": null,
"right": null
},
"right": {
"key": null,
"value": null,
"left": null,
"right": null
}
}
},
"right": {
"key": "Python",
"value": "Python is an interpreted, high-level, general-purpose programming language.",
"left": {
"key": null,
"value": null,
"left": null,
"right": null
},
"right": {
"key": "Ruby",
"value": "Ruby is a dynamic, interpreted, reflective, object-oriented, general-purpose programming language.",
"left": {
"key": null,
"value": null,
"left": null,
"right": null
},
"right": {
"key": null,
"value": null,
"left": null,
"right": null
}
}
}
}
}Nice! It works! It’s a little hard to read in this format, but knowing how strings are compared (“C++” < “Haskell” for example), the structure looks accurate! It might be good practice to verify this with the expected tree structure shown below:
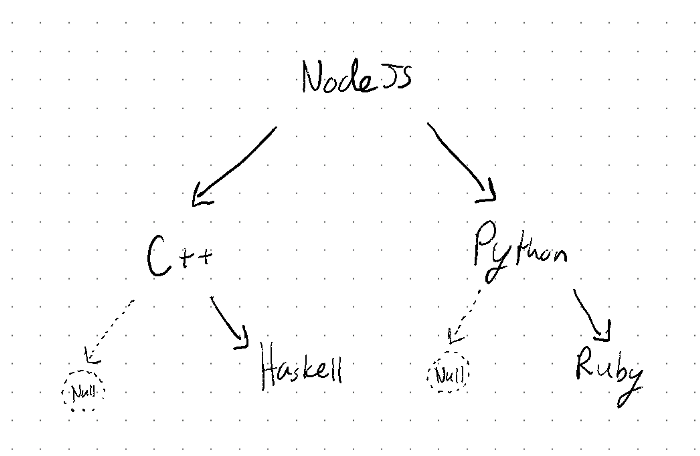
Implementing find:
Let’s pause for a moment to think about howfind will work. To find a node, we’ll need to recursively traverse the tree in a manner almost identical to what we did in the insert function with insertRecursive. We can easily copy-paste the same logic for find, but as a general rule of thumb, repeated code/logic is bad practice. If there’s a bug in one place, you’ll need to fix that bug in both functions, and it’s easy to forget to do that as a developer. In order to circumvent having to copy our logic, let’s refactor our insert code first by extracting the recursive tree traversal logic from insertRecursive into its own member function called findNode:
/* Internal helper function used to traverse the tree
and return the node with the key specified. If the
key does not exist in the tree, the node where the
key would be is returned. */
findNode(subRoot, key) {
if (subRoot.key === null || subRoot.key === key) {
/* If we reach an empty node, this will be our
insertion point, or if the key is what we are
looking for, return the target node. */
return subRoot;
} else {
/* We haven't reached an empty node or the target
node yet and need to recurse deeper... */
return (key < subRoot.key)
? this.findNode(subRoot.left, key)
: this.findNode(subRoot.right, key);
}
};
/* Inserts a new key/value pair into the BST. */
insert(key, value) {
/* Find insertion point and update key/value of Node
accordingly: */
const insertionNode = this.findNode(this.root, key);
insertionNode.value = value;
if (insertionNode.key === null) {
/* Only need to update key, left and right fields
if we're adding a new node to the tree */
insertionNode.key = key;
insertionNode.left = new BSTNode(null, null);
insertionNode.right = new BSTNode(null, null);
}
};Refactoring in this way makes our code a lot cleaner, shorter and more universal. By running the code once more, we see that the output is still what we expect it to be. Awesome! Let’s actually implement find now… It should be as simple as calling our findNode function and returning the value at that node. I’m also going to rename find to get to eliminate any confusion for the user between findNode and find:
/* Finds the data associated with the supplied
key. Returns NULL if no such key is present. */
get(key) {
return this.findNode(this.root, key).value;
};Note that this will return null in the case where a node with the specified key cannot be found in our tree since we are using ‘sentinel’ nodes to mark nonexistent leaves in our tree. Make sure to update the context binds in the constructor to reflect our name change and we should be ready to rumble!
Lets run our code once more, and it should spit out the definition for NodeJS:
NodeJS Definition: Node.js is an open-source, cross-platform JavaScript run-time environment that executes JavaScript code outside of a browser.
....Success! We’re almost done with all of the ADT functionality of a Binary Search Tree! All we need to do now is implement remove!
Implementing remove:
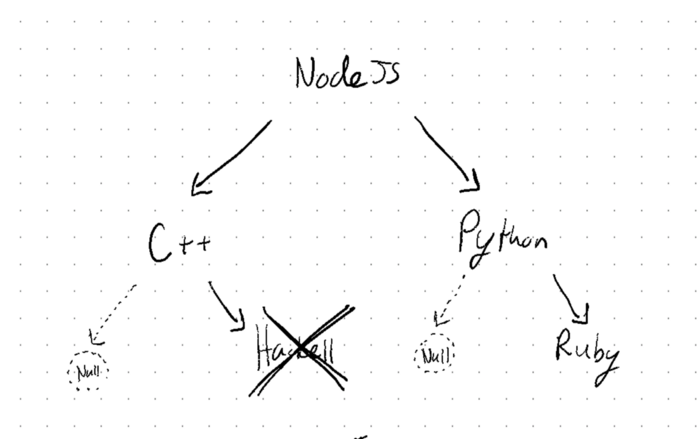
This one’s going to be a little tricky, so I saved it for last. Let’s take a qualitative look at how removals work in BSTs. There are three main cases for when we want to remove a node:
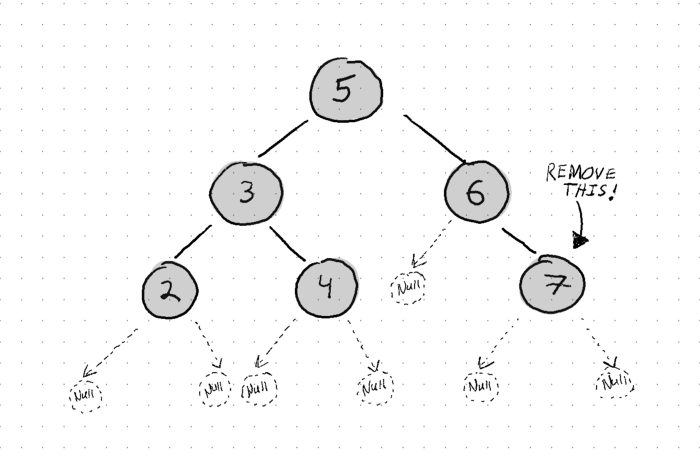
- The node we want to remove has no children. This one’s easy! Just replace it with one of our ‘dummy’ nodes to indicate that the leaf doesn’t exist!
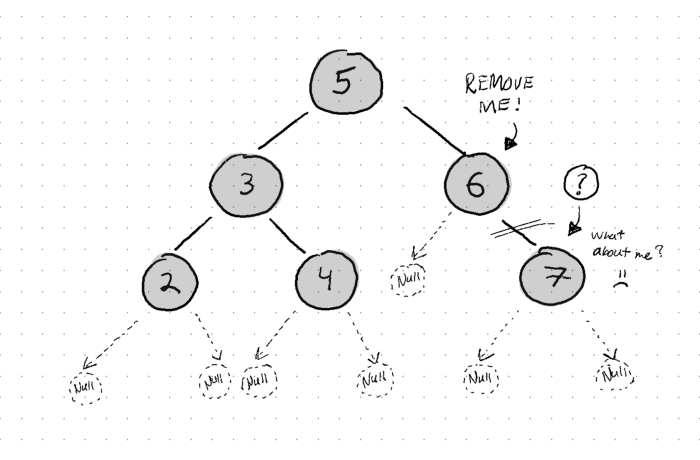
- The node we want to remove has one child. In this case, we take the one child and put it in the place of the node we want to remove. A little trickier, but still manageable.
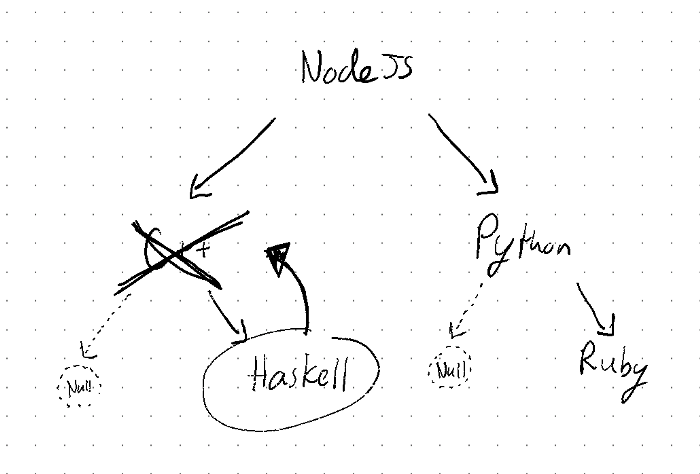
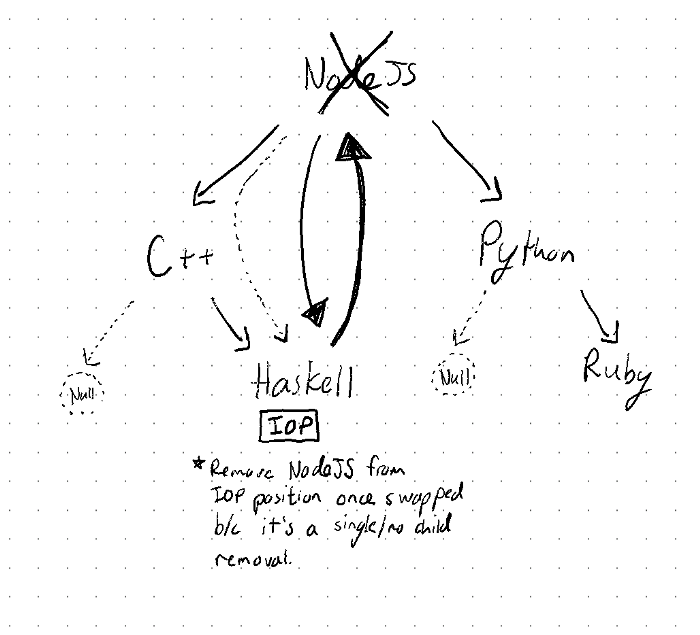
- Finally, we have the big bug-a-boo: removing a node with two children. Which one do we use to replace the node we’re removing? We can use the left/right child, but that could cause some balancing issues down the road. We’re traveling a bit into AVL Tree land here (self-balancing trees), but just stick with me as we take a leap of faith together. If we can locate the right-most child in the left sub-tree, we can essentially guarantee that this key will be bigger than all of the other nodes in the left sub-tree, but still smaller than anything in the right sub-tree. Take a moment to let this sink and look back at the definition of a Binary Search Tree. It’s really important to understand how this works. This node is so cool that we give it a very special name: The In-Order-Predecessor, or IOP.
Okay, that’s a lot of cases, and a lot to take in. Let’s start with the first two easier cases before focusing on two-child removal. Hopefully this can get our brain juices flowing before tacking the big daddy. Ready? Set. Code!
/* Removes data with supplied key from the BST. */
remove(key) {
const removalNode = this.findNode(this.root, key);
if (removalNode.key === null) return; /* does not exist */
const hasLeftChild = removalNode.left.key !== null;
const hasRightChild = removalNode.right.key !== null;
if (hasLeftChild && hasRightChild) {
/* Two child remove */
} else if (hasLeftChild && !hasRightChild) {
/* One child remove (left) */
} else if (!hasLeftChild && hasRightChild) {
/* One child remove (right) */
} else if (!hasLeftChild && !hasRightChild) {
/* No child remove */
removalNode.key = null;
removalNode.value = null;
removalNode.left = null;
removalNode.right = null;
}
};Testing this out by removing Haskell from our dictionary, we can see that this produces the expected result:
Tree: {
"root": {
"key": "NodeJS",
"value": "Node.js is an open-source, cross-platform JavaScript run-time environment that executes JavaScript code outside of a browser.",
"left": {
"key": "C++",
"value": "C++ is a general-purpose programming language.",
"left": {
"key": null,
"value": null,
"left": null,
"right": null
},
"right": {
"key": null,
"value": null,
"left": null,
"right": null
}
},
"right": {
"key": "Python",
"value": "Python is an interpreted, high-level, general-purpose programming language.",
"left": {
"key": null,
"value": null,
"left": null,
"right": null
},
"right": {
"key": "Ruby",
"value": "Ruby is a dynamic, interpreted, reflective, object-oriented, general-purpose programming language.",
"left": {
"key": null,
"value": null,
"left": null,
"right": null
},
"right": {
"key": null,
"value": null,
"left": null,
"right": null
}
}
}
}
}Now let’s handle the single child removal case(s):
/* Removes data with supplied key from the BST. */
remove(key) {
const removalNode = this.findNode(this.root, key);
if (removalNode.key === null) return; /* does not exist */
const hasLeftChild = removalNode.left.key !== null;
const hasRightChild = removalNode.right.key !== null;
if (hasLeftChild && hasRightChild) {
/* Two child remove */
} else if (hasLeftChild && !hasRightChild) {
/* One child remove (left) */
removalNode.key = removalNode.left.key;
removalNode.value = removalNode.left.value;
removalNode.right = removalNode.left.right;
removalNode.left = removalNode.left.left;
} else if (!hasLeftChild && hasRightChild) {
/* One child remove (right) */
removalNode.key = removalNode.right.key;
removalNode.value = removalNode.right.value;
removalNode.left = removalNode.right.left;
removalNode.right = removalNode.right.right;
} else if (!hasLeftChild && !hasRightChild) {
/* No child remove */
removalNode.key = null;
removalNode.value = null;
removalNode.left = null;
removalNode.right = null;
}
};Testing this against our dictionary of popular programming languages, we can see that removing C++ results in what we would expect:
Tree: {
"root": {
"key": "NodeJS",
"value": "Node.js is an open-source, cross-platform JavaScript run-time environment that executes JavaScript code outside of a browser.",
"left": {
"key": "Haskell",
"value": "Haskell is a standardized, general-purpose, purely functional programming language with non-strict semantics and strong static typing.",
"left": {
"key": null,
"value": null,
"left": null,
"right": null
},
"right": {
"key": null,
"value": null,
"left": null,
"right": null
}
},
"right": {
"key": "Python",
"value": "Python is an interpreted, high-level, general-purpose programming language.",
"left": {
"key": null,
"value": null,
"left": null,
"right": null
},
"right": {
"key": "Ruby",
"value": "Ruby is a dynamic, interpreted, reflective, object-oriented, general-purpose programming language.",
"left": {
"key": null,
"value": null,
"left": null,
"right": null
},
"right": {
"key": null,
"value": null,
"left": null,
"right": null
}
}
}
}
}Finally, let’s handle removing a node with two children. This is done by finding the IOP and then swapping it with our removal node. Because the IOP won’t have a right child (by definition), this will be either a single child removal or a no-child removal, both of which we have already accomplished above. Here is our final implementation of BST removal:
/* Removes data with supplied key from the BST. */
remove(key) {
const removalNode = this.findNode(this.root, key);
if (removalNode.key === null) return; /* does not exist */
const hasLeftChild = removalNode.left.key !== null;
const hasRightChild = removalNode.right.key !== null;
if (hasLeftChild && hasRightChild) {
/* Two child remove */
let iop = removalNode.left;
/* Select the left sub-tree's rightmost child as IOP */
while (iop.right.key !== null) iop = iop.right;
/* Swap removalNode with IOP */
removalNode.key = iop.key;
removalNode.value = iop.value;
/* Remove node now at position of IOP: */
if (iop.right !== null && iop.left !== null) {
if (iop.left.key !== null) {
/* One child removal on IOP (left) */
iop.key = iop.left.key;
iop.value = iop.left.value;
iop.right = iop.left.right;
iop.left = iop.left.left;
} else {
/* No child removal on IOP */
iop.key = null;
iop.value = null;
iop.left = null;
iop.right = null;
}
}
} else if (hasLeftChild && !hasRightChild) {
/* One child remove (left) */
removalNode.key = removalNode.left.key;
removalNode.value = removalNode.left.value;
removalNode.right = removalNode.left.right;
removalNode.left = removalNode.left.left;
} else if (!hasLeftChild && hasRightChild) {
/* One child remove (right) */
removalNode.key = removalNode.right.key;
removalNode.value = removalNode.right.value;
removalNode.left = removalNode.right.left;
removalNode.right = removalNode.right.right;
} else if (!hasLeftChild && !hasRightChild) {
/* No child remove */
removalNode.key = null;
removalNode.value = null;
removalNode.left = null;
removalNode.right = null;
}
};One thing you may note is that recursion could be used to delete the data at the IOP position on lines 15–34. This would reduce a lot of redundant code, but for some reason I wasn’t able to get this to work. If you’re able to figure this out, let me know and send a pull request (I’ve linked the GitHub repository at the end of this article)!
Testing this by removing the root node of our BST dictionary (NodeJS), we can see that our two-child removal case works swimmingly!
Tree: {
"root": {
"key": "Haskell",
"value": "Haskell is a standardized, general-purpose, purely functional programming language with non-strict semantics and strong static typing.",
"left": {
"key": "C++",
"value": "C++ is a general-purpose programming language.",
"left": {
"key": null,
"value": null,
"left": null,
"right": null
},
"right": {
"key": null,
"value": null,
"left": null,
"right": null
}
},
"right": {
"key": "Python",
"value": "Python is an interpreted, high-level, general-purpose programming language.",
"left": {
"key": null,
"value": null,
"left": null,
"right": null
},
"right": {
"key": "Ruby",
"value": "Ruby is a dynamic, interpreted, reflective, object-oriented, general-purpose programming language.",
"left": {
"key": null,
"value": null,
"left": null,
"right": null
},
"right": {
"key": null,
"value": null,
"left": null,
"right": null
}
}
}
}
}Whew. That was a lot. Are you still with me? Hopefully. We’ve just successfully implemented a Binary Search Tree in Javascript, and it only took about 100 lines of code (excluding my tendencies to comment everything under the sun)! Good job!
The whole codebase can be viewed via the repository linked at the end of the article.
Why Bother?
We just did something really cool, but will this really be useful in a high-level programming language like Javascript? The answer may be a lot less exciting than you’d probably like: it depends.
As mentioned previously, Binary Search Trees are really good at returning subsets of data within a given range. If you’re making an app that searches your data for nearby coffee shops, a BST might be a good idea if you built a KD-Tree on top of it. If you’re just looking for a quick and convenient place to store some of your working data, stick to using Javascript Objects and Arrays. They’re optimized by the V8 engine for almost all use-cases. Google knows what they’re doing.
const BST = require('./BST');
/* Benchmark Helper Lambda */
const BENCHMARK = (description, callback) => {
console.time(description);
callback();
console.timeEnd(description);
};
/* Performance testing: */
BENCHMARK("1M Tree insertions", () => {
const tree = new BST();
for (let i = 0; i < 1000000; i++) {
tree.insert(Math.random(), Math.random());
}
});
BENCHMARK("1M Javascript Object insertions", () => {
const testObj = {};
for (let i = 0; i < 1000000; i++) {
testObj[Math.random()] = Math.random();
}
});
BENCHMARK("1M Javascript Array insertions", () => {
const testArr = [];
for (let i = 0; i < 1000000; i++) {
testArr.push(Math.random());
}
});1M Tree insertions: 2129.266ms
1M Javascript Object insertions: 1870.163ms
1M Javascript Array insertions: 148.164msI will note though, however, that if we extended our Binary Search Tree to be self-balancing (aka an AVL Tree), our structure would probably match (if not beat) the insertion performance of regular Javascript Objects. This is pretty neat. We made a structure that has the potential to beat out one of the basic Javascript structures!



 Using Cache or not ?
Using Cache or not ?